¿Te has enfrentado alguna vez a operaciones con fracciones y no supiste por dónde empezar? No te preocupes, ¡no estás solo! La suma de fracciones y la sustracción de fracciones pueden parecer complicadas al principio, pero con una guía clara y práctica, lograrás dominarlas fácilmente.
En este artículo aprenderás paso a paso cómo sumar y restar fracciones con el mismo o diferente denominador, cómo identificar fracciones equivalentes, aplicar el mínimo común denominador, y resolver ejercicios reales para que compruebes tu progreso.
Además, conocerás las propiedades de la suma aplicadas a los números racionales, e incluso tendrás acceso a recursos útiles como explicaciones en video, prácticas guiadas y conceptos clave para no olvidar:

¿Qué es una fracción y por qué es tan importante?
Una fracción representa una parte de un total. En otras palabras, es una forma de dividir una cantidad en partes equivalentes. Está compuesta por dos números: el numerador (parte superior) y el denominador (parte inferior). Por ejemplo, en 3/5, el número 3 indica cuántas partes tomamos, y el 5 indica en cuántas partes se ha dividido el todo.
Las fracciones pertenecen al conjunto de los números racionales, es decir, todos aquellos que se pueden expresar como el cociente entre dos enteros.
Por otro lado, ¿sabes qué son los números racionales?
Saber manejar fracciones es esencial en muchos aspectos de la vida diaria: desde repartir comida hasta realizar cálculos financieros. Y cuando aprendes a hacer la suma y sustracción de fracciones, desbloqueas una herramienta fundamental de la aritmética.
¿Cómo sumar fracciones con igual denominador?
La forma más simple de sumar fracciones es cuando ambas tienen el mismo denominador, también conocidas como fracciones homogéneas. En este caso, la regla es muy sencilla: sumas los numeradores y mantienes el mismo denominador.
Ejemplo:
Supongamos que quieres resolver la siguiente operación:
5/9 + 2/9
Como los denominadores son iguales (9), se suman solo los numeradores:
5 + 2 = 7, por lo tanto el resultado es 7/9.
Este tipo de operación es muy útil para comenzar a entender cómo funcionan las fracciones.
¿Y si se trata de una resta de fracciones con igual denominador?
Funciona de la misma manera que la suma. Si los denominadores son equivalentes, solo tienes que restar los numeradores.
Ejemplo:
8/11 - 3/11 = (8 - 3) / 11 = 5/11
Así de fácil. Recuerda siempre verificar que el resultado no pueda simplificarse más. En este caso, 5/11 ya está en su mínima expresión.
Fracciones con distinto denominador: ¿cómo operar?
Aquí es donde muchos estudiantes comienzan a tener dificultades. Pero no te preocupes, lo importante es entender que no puedes sumar ni restar fracciones con distinto denominador sin antes igualarlos.
Para eso usamos el mínimo común denominador (MCD), que es el número más pequeño que es múltiplo común de los denominadores.
Ejemplo de suma con diferente denominador:
Vamos a sumar 2/3 + 1/4
El mínimo común denominador entre 3 y 4 es 12.
Convertimos ambas fracciones a un denominador común:
- 2/3 se convierte en 8/12 (porque 2x4 = 8)
- 1/4 se convierte en 3/12 (porque 1x3 = 3)
Ahora que tienen el mismo denominador, sumamos:
8/12 + 3/12 = 11/12
Ejemplo de sustracción con diferente denominador:
Resolvamos 5/6 - 2/9
El mínimo común denominador de 6 y 9 es 18.
Convertimos:
- 5/6 = 15/18 (5x3)
- 2/9 = 4/18 (2x2)
Ahora restamos: 15/18 - 4/18 = 11/18
Al igual que en la suma, el truco está en convertir ambas fracciones en fracciones equivalentes.


¿Cómo identificar fracciones equivalentes?
Una fracción equivalente es aquella que, aunque tiene números diferentes en el numerador y el denominador, representa la misma cantidad o porción de un todo. Este concepto es esencial para realizar procedimientos aritméticos, especialmente cuando se trabaja con fracciones de diferentes denominadores. Entenderlo bien te permitirá solucionar ejercicios con mayor soltura y precisión.
Por ejemplo, la fracción 1/2 es idéntica en valor a 2/4, 3/6 o 50/100. ¿Por qué? Porque todas indican la misma parte de un total, solo que expresadas con diferentes cifras. Si representaras cada una de estas fracciones en un gráfico circular, verías que todas ocupan exactamente la mitad del círculo.
¿Cómo se generan fracciones equivalentes?
Para obtener una fracción equivalente a otra, puedes aplicar un procedimiento muy sencillo: multiplicar o dividir ambos componentes (numerador y denominador) por el mismo número, siempre y cuando este sea diferente de cero.
Por ejemplo:
- Tomemos la fracción 3/5.
- Si multiplicamos tanto el numerador como el denominador por 2, obtenemos: 3×2 / 5×2 = 6/10
- Entonces, 3/5 y 6/10 representan la misma cantidad.
De forma similar:
- Si dividimos 12/16 entre 4, se obtiene: 12÷4 / 16÷4 = 3/4
Lo que estamos haciendo es “ampliar” o “reducir” la fracción sin alterar su valor real.
También: Descubre cómo se realiza la multiplicación de fracciones ¡aquí!
¿Por qué es útil este procedimiento?
El reconocimiento de fracciones equivalentes cumple varias funciones importantes:
🔹Uniformizar denominadores: cuando las fracciones tienen diferentes denominadores y necesitamos sumarlas o restarlas, es necesario convertirlas a una forma que permita compararlas directamente. Esto se logra encontrando versiones equivalentes con un denominador común.
🔹Simplificación de resultados: muchas veces, al finalizar una operación, obtenemos fracciones que pueden reducirse. Por ejemplo, si el resultado de una operación es 8/12, podemos simplificarlo dividiendo ambos términos entre 4, lo cual nos da 2/3.
🔹Comparación de cantidades: para saber cuál de dos fracciones es mayor, es útil convertirlas a equivalentes con el mismo denominador. Por ejemplo, si queremos comparar 2/3 y 3/5, podríamos convertirlas en 10/15 y 9/15, respectivamente. Así vemos que 2/3 es mayor.
Ejemplos de números racionales en la vida cotidiana.
Casos prácticos para familiarizarse
Para que el concepto quede aún más claro, veamos unos ejemplos adicionales:
¿5/8 y 20/36?
5×4 = 20
pero 8×4 = 32 ≠ 36
✖️ Entonces, 5/8 y 20/36
no son fracciones equivalentes.
¿3/7 y 6/14 son equivalentes?
Multiplicamos 3/7 por 2/2:
3×2 / 7×2 = 6/14
✔️ Sí, son equivalentes.
Multiplicación y otras operaciones con fracciones
Aunque nos centramos en la suma y la resta, es útil mencionar que también puedes multiplicar y dividir fracciones.
Multiplicación:
Para multiplicar, se multiplican los numeradores entre sí y los denominadores entre sí.
Ejemplo:
(3/4) x (2/5) = (3x2) / (4x5) = 6/20 = 3/10
División:
Para dividir una fracción entre otra, se multiplica la primera por el inverso de la segunda.
Ejemplo:
(2/3) ÷ (5/6) = (2/3) x (6/5) = (12/15) = 4/5

Propiedades de la suma en fracciones
Al trabajar con fracciones, es importante recordar que la suma sigue las propiedades generales de la aritmética:
- Propiedad conmutativa:
a/b + c/b = c/b + a/b
Ejemplo: 3/7 + 2/7 = 5/7 = 2/7 + 3/7 - Propiedad asociativa:
(a/b + c/b) + d/b = a/b + (c/b + d/b)
Ejemplo: (1/5 + 2/5) + 3/5 = 1/5 + (2/5 + 3/5) - Elemento neutro:
a/b + 0 = a/b
Estas reglas permiten hacer procedimientos más rápidamente y entender mejor cómo se comportan las fracciones.
Fracciones heterogéneas: ¿qué son y cómo se manejan
Las fracciones heterogéneas son aquellas con denominadores distintos. A diferencia de las homogéneas, requieren convertirlas previamente para poder operar.
Ya vimos cómo hacerlo con el mínimo común denominador, pero también existe la estrategia de la multiplicación cruzada cuando trabajamos con dos fracciones:
Ejemplo:
1/3 + 2/5
Multiplicamos cruzado:
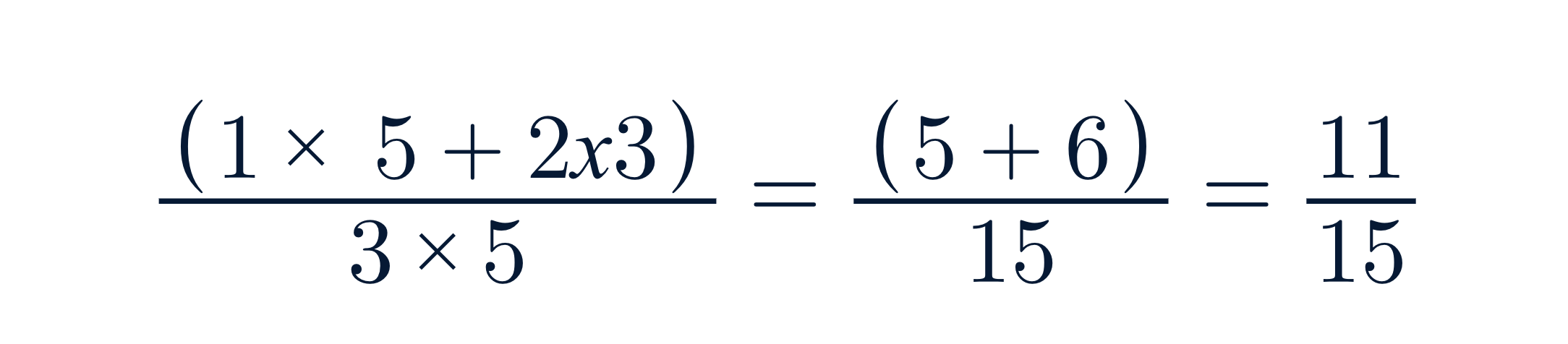
Este método puede ser muy útil cuando necesitas rapidez y no quieres calcular el MCD.
Suma y resta combinadas: ejercicios prácticos
En muchas situaciones tendrás que combinar ambos procedimientos . Por ejemplo:
Ejercicio:
(1/6 + 1/3) - 1/4
Primero, igualaremos denominadores. El MCD entre 6, 3 y 4 es 12.
Convertimos:
- 1/6 = 2/12
- 1/3 = 4/12
- 1/4 = 3/12
Ahora operamos:
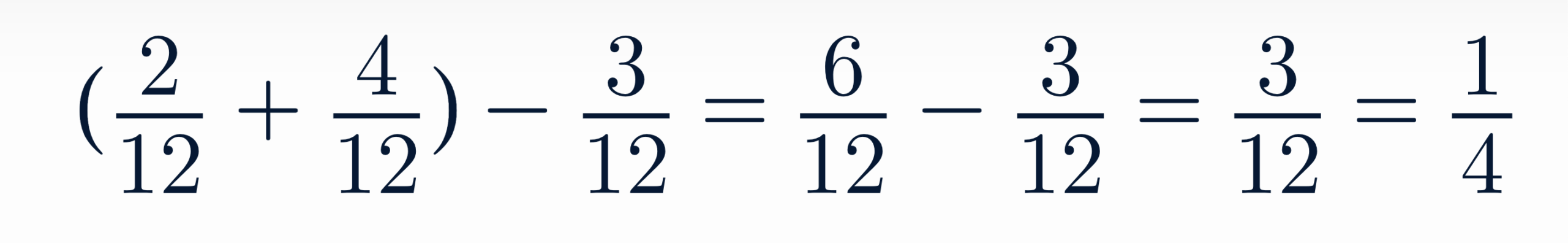
Este tipo de problemas es ideal para practicar todo lo aprendido.
Recursos recomendados para aprender fracciones
En la era digital, no estás solo para aprender. Existen múltiples herramientas para reforzar tu aprendizaje:
- Videos educativos en YouTube o plataformas como Khan Academy o Superprof.
- Calculadoras de fracciones online.
- Talleres interactivos o clases personalizadas en línea.
- Problemas de suma y sustracción de fracciones descargables o imprimibles.
En Superprof, contamos con docentes especializados que adaptan sus clases al nivel de cada alumno, desde primaria hasta preparación universitaria.
Puedes elegir clases presenciales u online y practicar con apoyo constante. Lo mejor es que puedes empezar con una primera clase gratuita o a tarifa mínima para conocer al profesor y su método.
¿Qué tanto conoces de las operaciones combinadas?
¡Seguro que ya lo entendiste! Aprender a realizar correctamente la suma y resta de fracciones te permitirá solucionar desde problemas escolares hasta cálculos en la vida diaria.
Recuerda aplicar el mínimo común denominador, identificar fracciones equivalentes, practicar con problemas variados y aprovechar los recursos en línea como videos, calculadoras y guías interactivas. También puedes buscar el apoyo de un profesor particular en Superprof, quien podrá explicarte paso a paso las propiedades de la suma, ayudarte con tus problemas de suma y sustracción de fracciones, y enseñarte cómo simplificar cualquier operación.
¿Listo para dominar los números racionales? ¡Empieza hoy!
Resumir con IA:















