«Todo número iluminado tiene su sombra dorada». - Nabil Alami
El número áureo, también conocido como razón dorada, proporción áurea o proporción divina, es una relación matemática que se define como el valor numérico que guardan dos segmentos de una recta, a y b, siendo a más largo que b. La longitud total formada por la suma de los segmentos a y b se relaciona con el segmento más largo a de la misma manera en que este último se relaciona con el segmento más corto b: (a + b)/a = a/b.
Este número también se representa con la letra griega ? (phi) y es un número irracional que se obtiene como la única solución de la ecuación x^2 = x + 1. Su valor aproximado es alrededor de 1,6180339887.
En el ámbito educativo, son numerosos los estudiantes que acuden a clases particulares, y muchos de ellos eligen las matemáticas como materia de estudio. Aunque las matemáticas suelen considerarse una asignatura desafiante, también pueden resultar fascinantes y albergar enigmas cautivadores. En esta ocasión, exploraremos uno de ellos: el enigmático número áureo.
Descubre con Superprof Perú todo sobre los números más famosos de las matemáticas.

La historia del número áureo

El origen del número áureo
La icónica pirámide de Keops, construida alrededor del año 2600 a.C., es considerada por muchos científicos como el punto de partida de la proporción áurea.
El número áureo tiene una antigüedad notable y su uso inicial se encontraba en el ámbito de la geometría, posiblemente por parte de los pitagóricos. Ellos emplearon esta proporción para la construcción de pentágonos utilizando triángulos isósceles. En aquel entonces, no se le otorgaba un uso aritmético, ya que los pitagóricos creían que todos los números eran racionales. Sin embargo, el número áureo demostró ser una excepción a esta creencia, al ser un número irracional.
Pero en realidad el primer texto matemático que hace referencia al número áureo fue escrito por Euclides (300 a.C.), que lo define de la siguiente manera: «se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor».
Sin embargo, si retrocedemos aún más en el tiempo desde el primer texto descubierto, podemos encontrar los orígenes del estudio de la proporción divina. Platón, sin lugar a dudas, desempeña un papel fundamental en el estudio de la proporción áurea como objeto de investigación por mérito propio. En aquel entonces, este número no recibía el nombre de "número áureo".
¿Quieres saber más sobre el número e?
El número áureo en la Edad Media
En el siglo VIII, el matemático, astrónoma y geógrafo persa Al-Khawarizmi aportó una nueva perspectiva a la proporción dorada al plantear varios problemas que involucraban la división de una longitud de diez unidades en dos partes. La solución a uno de estos problemas resultó ser el tamaño inicial dividido por el número áureo.
Sin embargo, fue Fibonacci quien introdujo las ecuaciones del matemático persa en Europa, especialmente a través de su famosa sucesión de Fibonacci, aunque en ese momento no se estableció una conexión explícita con la proporción áurea.
La demostración de la irracionalidad del número áureo fue llevada a cabo por Campanus de Novara, un matemático, astrónomo, astrólogo y médico italiano, mediante el análisis del descenso infinito que se puede observar en la espiral dorada.
El número áureo durante el Renacimiento
Durante el Renacimiento, al número áureo se le conoce como la divina proporción y se le atribuye una intervención divina, según lo expuesto en el libro del matemático y franciscano italiano Luca Pacioli, cuyas ilustraciones son reconocidas gracias al famoso Leonardo da Vinci.
Fue en esta misma época cuando se establece una conexión entre la sucesión de Fibonacci y el número áureo. Al dividir un término de la sucesión por su término anterior, el resultado tiende a acercarse al número áureo. Esta aproximación se vuelve más precisa a medida que los términos de la sucesión son más grandes.
El descubrimiento de esta relación se produjo a través de una nota anónima, pero el astrónomo y matemático alemán Johannes Kepler fue quien realmente lo encontró, quedando fascinado por el número áureo a lo largo de toda su vida.
¿Te interesa conocer también el número 0?
El nacimiento de un mito en el siglo XIX
En este siglo, el número áureo pierde su relevancia matemática, pero gana cada vez más importancia como un sistema en sí mismo.
El filósofo alemán Adolf Zeising sostiene que la proporción áurea puede brindar una comprensión tanto en el ámbito científico como en el artístico. Aunque sus teorías tienen un enfoque científico cuestionable, encuentran aceptación, especialmente en Francia. Se argumenta que la belleza puede ser explicada gracias al número áureo.
Incluso a lo largo del siglo XX, el número áureo continúa fascinando a matemáticos, artistas y arquitectos.
Lee también nuestro artículo sobre los números perfectos.
El número áureo en geometría
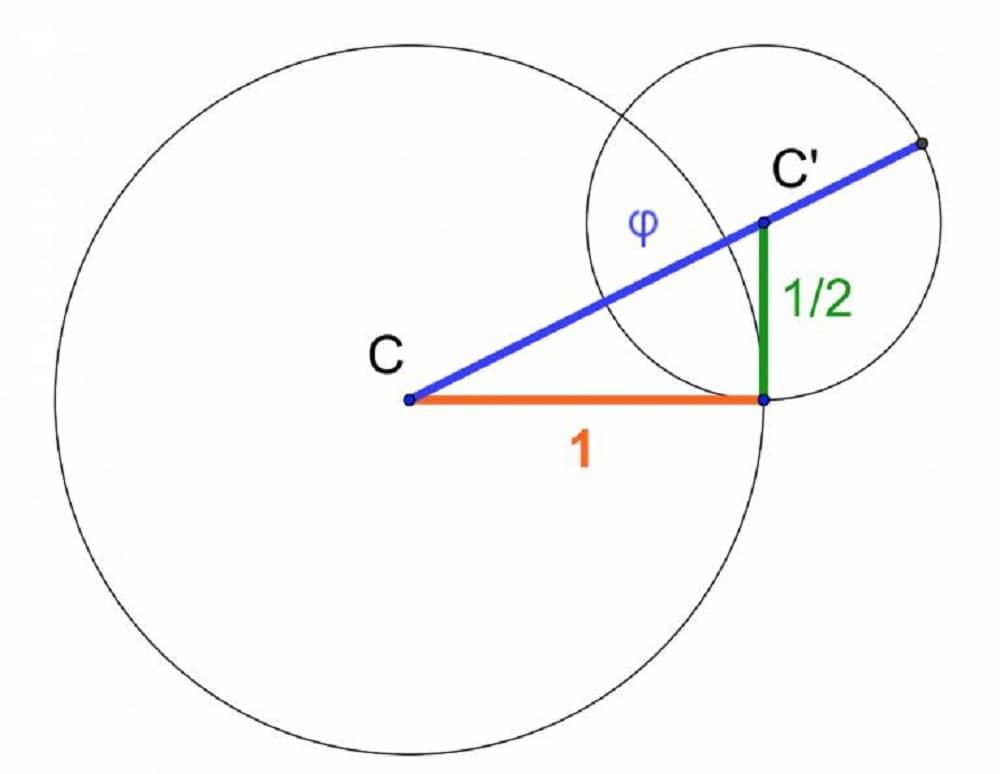
La primera definición de la proporción áurea se establece en términos geométricos. El teorema establece lo siguiente: "Dos longitudes a y b (ambas estrictamente positivas) cumplen la proporción áurea si la relación entre a y b es igual a la relación entre la suma de a y b y a".
A la luz de los trabajos de Euclides, surge una nueva definición de proporción áurea:
«El número áureo es el número real positivo, denotado por ?, igual a la fracción a/b si a y b son dos números en proporción de extrema y media razón».
Esta es la fórmula correspondiente: ? = (1 + ?5) / 2.
? es la solución de una ecuación de segundo grado, que da una tercera definición: «El número áureo es la única solución de la ecuación x2 – x – 1 = 0».
Mediante estos cálculos, se puede trazar una proporción de extrema y media razón utilizando herramientas como un compás, una regla y una escuadra.
- Dibuja un círculo C de radio 1.
- Al final del radio 1, dibuja un segmento de longitud 1/2, perpendicular al radio.
- Dibuja el círculo C’ de radio 1/2 colocando la punta del compás al final del segmento de longitud 1/2 previamente dibujado.
- Dibuja el segmento desde el centro del círculo C hasta el final del círculo C’, pasando por el centro del círculo C’.
- La longitud de este segmento tiene el valor del número áureo.
A partir de estos círculos, puedes construir un rectángulo áureo.
Además, es posible incluir un cuadrado con un lado de longitud a - b dentro del rectángulo áureo de lados b × (a - b). Al agregar un cuarto de círculo en cada cuadrado, se obtiene una espiral conocida como espiral dorada.
La proporción áurea también se aplica en la construcción de pentágonos y pentagramas, así como en el campo de la trigonometría.
Echa un ojo también a nuestro artículo sobre el número i.
Descubre nuestra oferta de clases particulares matemáticas en Superprof Perú.

El número áureo en aritmética

¿Para que sirve el numero áureo? El número áureo puede ser definido de manera algebraica como la única raíz positiva de una ecuación. También se puede utilizar un enfoque algebraico-geométrico para resolver una ecuación de segundo grado, denominado álgebra geométrica. La ecuación ?^2 = 1 + ? tiene como solución el número áureo.
Además, la proporción áurea puede ser obtenida mediante el uso de fracciones continuas infinitas, como 1 + (1/(1 + (1/1))).
La sucesión de Fibonacci también provee aproximaciones del número áureo.
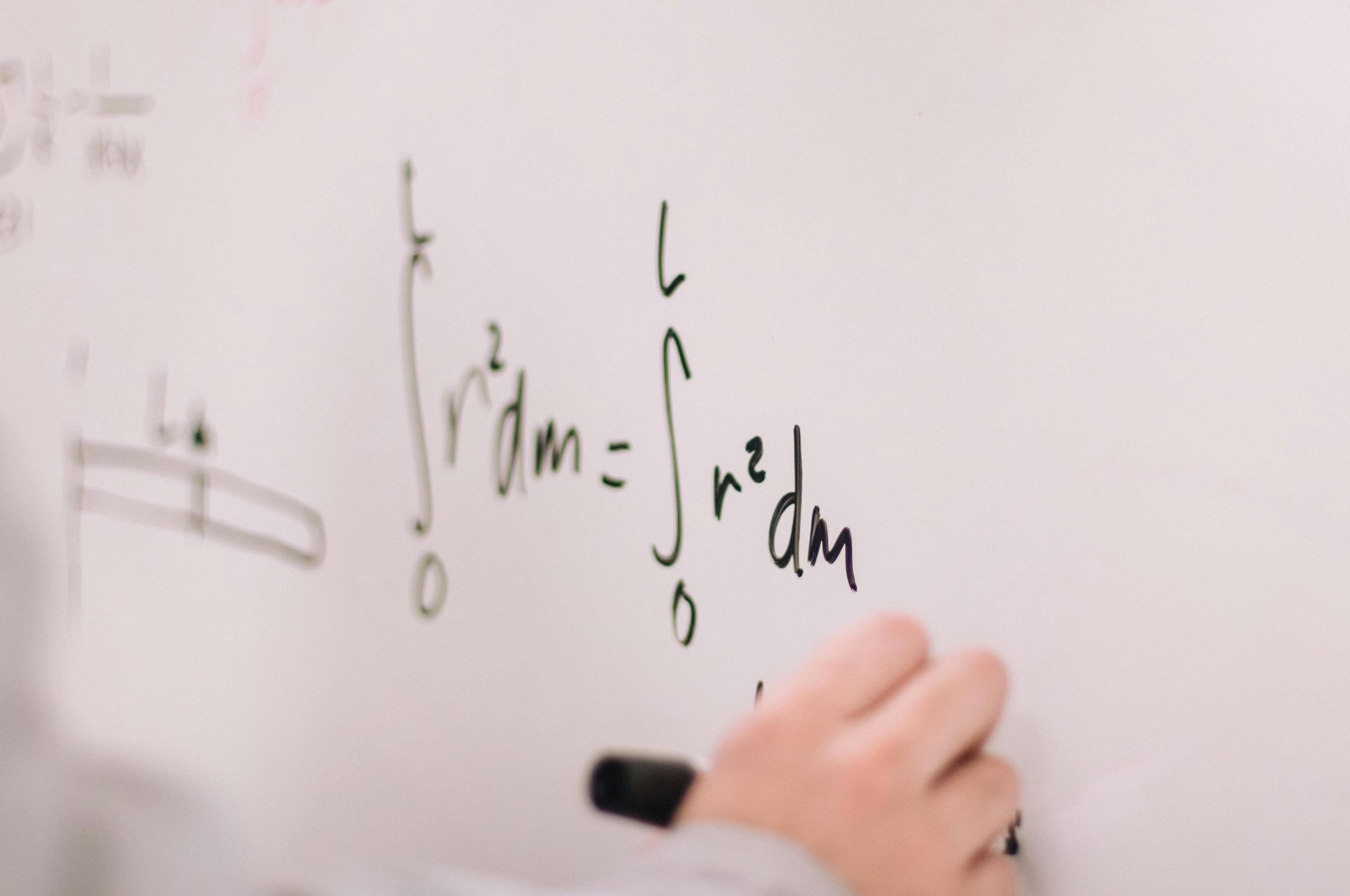
La fórmula de Binet permite expresar la sucesión de Fibonacci en términos de la proporción áurea.
Además, el número áureo encuentra aplicación en algunas ecuaciones diofánticas.
Por cierto, ¿ya lo sabes todo sobre el número Pi?
¿Te gustaría descubrir opciones de cursos de matemáticas online?
La omnipresencia del número áureo
El número áureo se encuentra en todas partes, tanto en el ámbito de las matemáticas como en nuestro entorno. En la naturaleza, podemos observar la presencia de la proporción dorada en diversos elementos:
- Las escamas de una piña de pino generan espirales logarítmicas que pueden producir la sucesión de Fibonacci.
- Los estambres de un girasol responden al mismo fenómeno.
- Los cristales de cuarzo se forman en un patrón pentagonal, en el que interviene el número áureo.
- La corteza de una piña induce una espiral ordenada asociada con la proporción áurea.
Sin embargo, en el caso de la disposición de las hojas en el girasol y la estructura cristalina del cuarzo, no siempre se siguen estrictamente las reglas de la proporción áurea, lo que hace difícil atribuirles un carácter místico o divino. Es posible que sea simplemente una coincidencia.

La cuestión de si existe una conexión entre el cuerpo humano y la proporción áurea ha sido objeto de debate en numerosos contextos, ya sea en el ámbito científico, artístico o estético.
En su momento, Zeising intentó medir el cuerpo humano utilizando únicamente el número áureo, pero rápidamente descartó esta idea al encontrar que las proporciones resultantes no eran realistas. Además, las dimensiones del cuerpo humano son variables y cambian constantemente a lo largo del crecimiento y desarrollo, sin seguir necesariamente un patrón uniforme.
A pesar de esto, la búsqueda de la proporción dorada en el cuerpo humano no ha sido abandonada por completo. Actualmente, los científicos enfocan sus investigaciones en el cerebro en busca de posibles vínculos con la proporción áurea, aunque esta teoría sigue siendo controvertida y objeto de discusión.
Además de su interés para los científicos, la proporción dorada también ha capturado la atención de diversos campos, como la pintura, especialmente durante el Renacimiento. En aquel período, al número áureo se le denominaba divina proporción, y podemos encontrar su presencia en obras artísticas como el cuadro "El nacimiento de Venus" de Botticelli.
Sin embargo, en ocasiones se plantean interpretaciones posteriores y no se puede atribuir una intención consciente por parte del artista, como se sugiere en el caso del cuadro de San Jerónimo de Leonardo da Vinci, donde se encuentra presente el rectángulo áureo.
El uso de la proporción áurea en numerosas construcciones antiguas es un tema que genera controversia. Es difícil determinar si los constructores tenían conocimiento y utilizaban conscientemente la proporción áurea, o si se trata de una interpretación excesiva por parte de los arqueólogos.
Hay varios ejemplos:
- El teatro de Epidauro (Grecia, siglo IV a. C.).
- La gran pirámide de Guiza (Egipto, siglo XXVI a. C.).
- La fachada del Partenón según las convenciones (Grecia, 447-432 a. C).
- El gran altar de Pérgamo (actual Turquía, 188 a. C., conservado en Alemania).
Explora nuestra amplia selección de cursos de matemáticas desde nivel básico y descubre al profesor de matemáticas perfecto para ti en Superprof Perú.
En el siglo XX, el renombrado arquitecto suizo Le Corbusier (Charles-Édouard Jeanneret-Gris) desarrolló una teoría sobre el uso de la proporción áurea y creó un sistema de medidas detallado conocido como Le Modulor. Siguiendo los pasos de pensadores como Da Vinci, Le Corbusier buscaba establecer una relación matemática entre las dimensiones humanas y la naturaleza. El Modulor fue aplicado en numerosas construcciones del arquitecto, como la "ciudad radiante" en Marsella o la capilla de Notre-Dame-du-Haut en Ronchamp.
Este fenómeno no se limita solo a lo visual, sino que también se puede aplicar al ámbito auditivo. En la música, se busca la presencia del número áureo en la armonía y el ritmo. Una aproximación cercana al número áureo es la sexta menor, obtenida mediante la relación de frecuencias 8/5 = 1.6.
La fascinación por la presencia del número áureo es amplia y ha dado lugar a teorías científicas y comprobadas, aunque algunas más sólidas que otras. Algunos lo han denominado "el número de Dios" debido a su aparente ubicuidad en diversos ámbitos.
¿Conocías la proporción áurea? Descubre también la historia de los números primos.
La sucesión Fibonacci
Este artículo menciona repetidamente la sucesión de Fibonacci y su estrecha relación con la proporción áurea. ¿Te ha cautivado todo lo que te hemos contado sobre este fascinante concepto del número áureo? Una vez que descubras su presencia, lo verás en todas partes.
Fibonacci es el seudónimo del matemático italiano Leonardo de Pisa (1170-1240). Este erudito contribuyó a difundir el sistema de numeración indo-arábiga en Europa, ya que hasta entonces se utilizaba el sistema de numeración romana. Además, fue el primero en describir la secuencia numérica que ahora lleva su nombre.
¿Estás en la búsqueda de clases privadas de matemáticas en Perú? ¡Descubre las opciones disponibles en Superprof Perú!

La sucesión Fibonacci es una secuencia infinita de números naturales que comienza con 0 y 1. Sin embargo, el siguiente número no es 2. En esta secuencia, cada número es la suma de los dos anteriores. Entonces, después de 0 y 1, obtenemos 0 + 1 = 1. Por lo tanto, la sucesión continúa: 0, 1, 1. Para encontrar el siguiente número, sumamos los dos últimos de la secuencia: 1 + 1 = 2. Así que la secuencia se convierte en: 0, 1, 1, 2. Este patrón continúa de la misma manera. Los primeros números de esta secuencia son:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 114, 233, 377, 610, 987, 1597, 2554, 4151...
Capisci?
La lista es infinita.
De esta manera, cada uno de los números que conforman esta secuencia se conoce como los números de Fibonacci.
Esta serie tiene aplicaciones en diversos campos del conocimiento, como la informática, las matemáticas o la teoría de juegos. Sin embargo, lo realmente asombroso es cómo podemos encontrarla en la naturaleza. En este sentido, nos recuerda a la proporción dorada, ya que se desvincula de lo estrictamente matemático y la observamos en los elementos que nos rodean. ¿Quién podría imaginar que la disposición de las hojas de una alcachofa sigue una secuencia lógica que coincide con la sucesión de Fibonacci? Lo mismo ocurre con partes de girasoles, brócolis o piñas.
Aunque encontramos registros de esta secuencia mucho antes en la historia. Parte del mérito también se atribuye a pensadores como el matemático indio Pingala (que se cree que vivió en el siglo III a.C.), el prosodista y matemático indio Virahanka (siglo VI o VII) y Jema Chandra, un polímata y poeta indio.
La sucesión, tal como la describió y dio a conocer Leonardo de Pisa, fue desarrollada como una solución a un problema relacionado con los hábitos de apareamiento de los conejos. Sí, se dice que Fibonacci descubrió esta secuencia al contar conejos. En ese momento, los pensadores y ganaderos no lograban comprender la lógica detrás de la reproducción de los conejos. Partiendo de la premisa de que inicialmente tienes una pareja, ¿cómo saber cuántas parejas tendrás después de x meses, sabiendo que cada mes una pareja puede reproducirse y obtener otra pareja? Es importante tener en cuenta que los conejos tardan un mes en alcanzar la madurez para poder reproducirse. A continuación, podrás consultar cómo se desarrolla el nacimiento de nuevas parejas mes a mes y cómo calcular el número de parejas que tendrás.
Si estás interesado en encontrar clases particulares de matemáticas en Lima, Superprof Lima es el sitio ideal para ti.

La sucesión de Fibonacci y la reproducción de los conejos.
La naturaleza es increíble.
Al comenzar el primer mes, nace la primera pareja de conejos (pareja A). Al finalizar el mes, la pareja alcanza la madurez reproductiva y da a luz a la pareja B, mientras que la pareja A se cruza nuevamente. En este punto, tenemos un total de 2 parejas. Al finalizar el tercer mes, la pareja A da a luz a la pareja C, mientras que la pareja B alcanza un mes de edad. Se cruzan las parejas A y B, y tenemos un total de 3 parejas. Al finalizar el cuarto mes, las parejas A y B dan a luz a las parejas D y E, respectivamente. La pareja C cumple un mes. Se cruzan las parejas A, B y C, y tenemos un total de 5 parejas. En el quinto mes, las parejas A, B y C dan a luz a las parejas F, G y H, respectivamente. Las parejas D y E cumplen un mes. Se cruzan las parejas A, B, C, D y E, y tenemos un total de 8 parejas. En el sexto mes, las parejas A, B, C, D y E dan a luz a las parejas I, J, K, L y M, respectivamente. Las parejas F, G y H cumplen un mes. Se cruzan las parejas A, B, C, D, E, F, G y H, y tenemos un total de 13 parejas. Este patrón continúa de manera similar en los meses siguientes. Aunque puede resultar confuso al leerlo de forma secuencial, al visualizarlo con papel y lápiz o mediante imágenes, se aclara fácilmente.
Como hemos mencionado anteriormente, esta sucesión de Fibonacci no solo se aplica a la reproducción de los conejos, sino que también parece repetirse en numerosos aspectos de la naturaleza. De hecho, algunos podrían considerar a los números de Fibonacci como los números favoritos de la naturaleza.
Un dato sorprendente es que si divides cualquier número de Fibonacci por el número que le precede, por ejemplo, 55 dividido por 34 (= 1,617), 21 dividido por 13 (= 1,615), 5 dividido por 3 (= 1,66), o 610 dividido por 377 (= 1,62), la respuesta siempre es cercana a 1,61. ¿No te parece fascinante? Es por esta razón que la secuencia de Fibonacci también es conocida como la secuencia dorada, haciendo referencia a esta aproximación constante a 1,61.
Además, este número que resulta de las divisiones, específicamente 1.61803, se conoce como el número áureo o número de oro. Como mencionamos anteriormente, en matemáticas se representa con la vigésima primera letra del alfabeto griego, phi, ? (en mayúsculas ?).
Cuando aplicamos este número phi a las proporciones de un rectángulo, obtenemos lo que se conoce como un rectángulo dorado. Se considera que este rectángulo es una de las formas geométricas más estéticamente satisfactorias. Y como era de esperar, a partir de este rectángulo dorado se genera otro elemento relacionado con el oro: la llamada espiral dorada. Esta espiral se forma al crear cuadrados adyacentes con dimensiones basadas en la sucesión de Fibonacci. Es como la perfección dentro de la perfección.
¿Estás interesado en encontrar clases particulares de matemáticas en Perú? ¡Puedes confiar en Superprof Perú!

Llámalo número áureo, razón extrema y media, razón dorada, proporción áurea, media áurea o divina proporción, pero este fenómeno seguramente te maravillará.
¿No te ha impresionado todo lo que te hemos contado hasta ahora? Aún hay más. Incluso en tu propio cuerpo encontrarás estos números áureos. No es casualidad que se le llame el número de Dios, ya que está presente en todas partes. Veamos algunos ejemplos:
-La distancia desde el ombligo hasta los pies y desde la parte superior de la cabeza hasta el ombligo sigue la proporción áurea.
-Una molécula de ADN tiene dimensiones de 34 angstroms x 21 angstroms en cada ciclo completo de la doble hélice. Estos números, 34 y 21, son sucesivos en la sucesión de Fibonacci.
-En los dedos, cada sección desde la punta hasta la base es más grande que la anterior en aproximadamente la proporción del número phi.

Estos son hechos interesantes, pero también hay muchas conjeturas al respecto. Se sostiene que el cerebro humano muestra preferencia por objetos e imágenes que contienen la proporción áurea. ¿Cuál es tu opinión al respecto?
Además, se afirma que nos sentimos más atraídos por caras que exhiben proporciones áureas entre el ancho de la cara y el ancho de los ojos, la nariz y las cejas. ¿Alguna vez te has preguntado por qué ciertas características faciales son consideradas más "atractivas" que otras? ¿Coincide esto con lo que hemos descrito anteriormente?
Explora nuestra oferta de clases de matemáticas en línea y descubre todo lo que tenemos para ofrecerte.
Resumir con IA:
















