«La verdad está hecha para las matemáticas, la química, la filosofía, pero no para la vida» - Ernesto Sabato (1911-2011)
Dominar los ejercicios matemáticos se convierte en una proeza técnica para muchos estudiantes, desde la escuela primaria hasta la universidad. Desde el fascinante mundo de los logaritmos naturales hasta las intrigantes funciones exponenciales, desde el intrincado álgebra hasta la cautivadora geometría, a veces resulta desafiante visualizar las matemáticas de manera tangible.
Dentro de este panorama, las clases de matemáticas no siempre son tan tangibles, y esto se hace evidente cuando nos encontramos con el número "i". Como uno de los números complejos, su uso en matemáticas puede parecer enigmático y exigente.
En el último Informe PISA, llevado a cabo en 2015, los resultados mostraron que los estudiantes de países asiáticos sobresalen en matemáticas en comparación con sus contrapartes europeas, mientras que en América Latina se obtuvieron las puntuaciones más bajas. En este artículo, Superprof Perú se adentra en el intrigante mundo de un número irracional en álgebra: ¡El número "i"!
Descubre con nosotros los números más famosos de las Matemáticas.

El álgebra, una parte importante de las Matemáticas
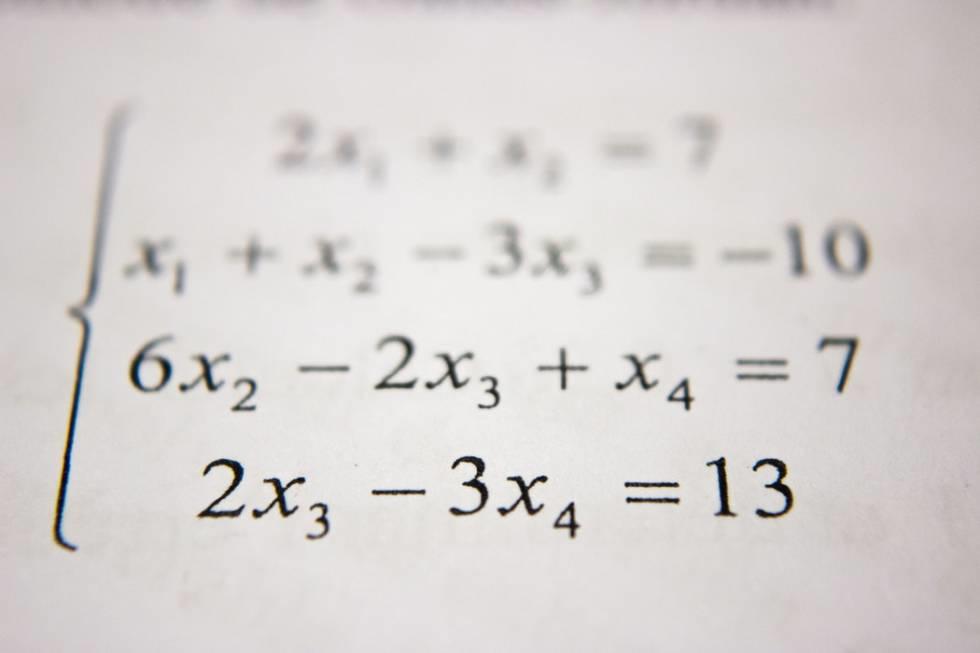
En el vasto campo de las matemáticas, los números desempeñan un papel fundamental e indispensable. Sin embargo, es evidente que no todas las cifras se utilizan de la misma forma, ya que una suma y los números complejos no poseen las mismas propiedades. De hecho, algunos números son más intrincados que otros. En general, podemos distinguir diversas disciplinas dentro del ámbito del álgebra, cada una con su propio nivel de complejidad.
- El álgebra no conmutativa.
- La nueva álgebra.
- La aritmética.
- El cálculo formal.
- La geometría algebraica.
- El álgebra homológica.
- El álgebra lineal.
- La estructura algebraica.
- El teorema del álgebra.
¡Y muchas otras disciplinas!
El uso de los números abarca una amplia gama de aplicaciones y requiere un aprendizaje minucioso. En el ámbito del álgebra, solo explorar todo su programa llevaría incontables horas. Sin embargo, existen ciertos dominios, como los números imaginarios, que poseen propiedades extraordinarias y, por definición, complejas. ¿Deseas adentrarte en este fascinante mundo? ¡Entonces, avancemos sin vacilar!
Precisamente, en su forma algebraica, los números complejos se representan mediante la siguiente fórmula:
a + ib
El número a representa la parte real, mientras que la parte b se refiere a la parte imaginaria.
Antes que nada, es importante comprender que los números complejos engloban tanto a los números reales como a los números imaginarios. De manera más precisa, se utilizan las siguientes denominaciones:
- N = conjunto de números naturales.
- Z = conjunto de enteros relativos.
- D = conjunto de decimales.
- Q = conjunto de racionales.
- R = conjunto de reales.
- C = conjunto de complejos.
Explora las clases de matemáticas de nivel primario disponibles en nuestra plataforma.
El número imaginario puro, conocido como "i", es una componente fundamental en el campo de los números complejos, representando la raíz cuadrada de -1. En este artículo, te adentraremos en los secretos y maravillas de este fascinante número.
¡Vamos a meternos de lleno en el tema!
¿Quieres saber más sobre el número e?
El número i: propiedades y definición
¿Qué es un numero imaginario en matemáticas?

El número imaginario "i" se establece en el campo de las Matemáticas como un número complejo que puede asimilarse de manera relativamente sencilla, pero que requiere habilidades de abstracción. Permíteme explicarlo de forma más detallada:
En el ámbito matemático, algunas ecuaciones de segundo grado carecen de solución real debido a la inexistencia de un número real cuyo cuadrado sea negativo. Esto implica que no se puede obtener un resultado positivo al multiplicar un valor por sí mismo. Por ejemplo, 2² es igual a 4, al igual que (-2)².
Para entender esta propiedad matemática, es necesario regresar a las lecciones de Matemáticas de la educación primaria, donde se nos enseña la regla de los signos: sumar, restar, multiplicar o dividir un número positivo por otro positivo resulta en un número positivo; multiplicar un número negativo por uno positivo o viceversa da como resultado un número negativo; y multiplicar dos números negativos produce un número positivo.
Siguiendo este teorema matemático que establece el producto de dos números negativos como positivo, podemos concluir que el cuadrado de cualquier número, incluso uno negativo, resulta en un número positivo.
En el año 4, dentro del ámbito de las figuras geométricas, el teorema de Pitágoras y Tales, se establece la definición de las raíces cuadradas de la siguiente manera: la raíz cuadrada de un número x es aquel valor que, al ser elevado al cuadrado, resulta en x. En términos algebraicos, si n es igual a la raíz cuadrada de x, entonces n² es igual a x. Por ejemplo, si x = 9, entonces n = 3.
¿Cuál es el propósito de esta explicación? A lo largo de los siglos de desarrollo en el campo de las Matemáticas, la necesidad de encontrar raíces cuadradas de números negativos condujo a la creación de los números complejos, representados por la unidad imaginaria i.
Los números complejos se definen como una extensión del conjunto de números reales, incluyendo un componente imaginario representado por la unidad imaginaria i, con propiedades como i = raíz cuadrada de -1 y i² = -1. Incluso el cuadrado de (-i) también es igual a -1.
La idea principal es que cualquier número puede expresarse en la forma a + ib, donde a y b son números reales, positivos o negativos. Por ejemplo, la raíz cuadrada de -4 se puede escribir como 2i.
Los números que siguen la fórmula bi, donde b es distinto de cero, son conocidos como números imaginarios puros. Es por eso que expresiones como "raíz cuadrada de -4 = 2i" y "raíz cuadrada de -16 = 4i" son ejemplos de números imaginarios.
Si no existe la raíz cuadrada de -1, no podemos calcular de manera precisa o aproximada decimales como lo hacemos con las raíces de números positivos (por ejemplo, la raíz cuadrada de 5 es aproximadamente 2.236).
El número imaginario "i" es un concepto que nos permite visualizar y comprender una amplia gama de raíces elevadas al cuadrado de números negativos.
Preguntas:
- ¿Qué número obtenemos si elevamos 3i al cuadrado?
- ¿Cuál de estos dos números tiene un cuadrado de -16 (-4 o 4i)?
(Las respuestas están al final del artículo).
¿Te interesa conocer también el número 0?
La historia del número i
En el siglo XVI, el surgimiento de los números complejos se dio gracias a los avances matemáticos de Gerolamo Cardano, un destacado matemático italiano, quien los utilizó para resolver ecuaciones de tercer grado.
Posteriormente, Raphael Bombelli se convirtió en el primer matemático en desarrollar reglas de cálculo para los "números imposibles" en el álgebra, sentando las bases de las propiedades de los números complejos.
El número i se origina a partir de la búsqueda de soluciones no reales para ecuaciones de tercer grado, ecuaciones polinomiales con una raíz cúbica.
En 1637, el filósofo René Descartes acuñó el término "números imaginarios" para referirse a estos valores imposibles. Más tarde, en 1777, la notación "i" fue introducida por Leonhard Euler, quien también desarrolló el número "e" para calcular la función exponencial.
Durante el siglo XIX, gracias a los trabajos de C.F. Gauss, los números complejos imaginarios puros fueron reconocidos como números legítimos por derecho propio.
El interés de los números complejos, como "e" e "i", radica en su capacidad para representar de manera concisa resultados aparentemente complicados. Según Augustin Louis Cauchy, permiten expresar combinaciones de signos algebraicos que no tienen un significado propio, pero que simplifican enormemente las expresiones matemáticas.
¿Estás en busca de un profesor de matemáticas? Encuentra al Superprof Perú ideal para ti en nuestra plataforma.
Para facilitar el cálculo algebraico, también se introducen los números complejos en la representación geométrica para facilitar los cálculos.
Por cierto, ¿ya lo sabes todo sobre el número Pi?

¿Cuál es la utilidad de emplear los números imaginarios puros?
Aunque los cálculos con números imaginarios puedan parecer menos relevantes en ejercicios matemáticos para preparar exámenes, los números complejos tienen una amplia gama de aplicaciones y usos en diferentes campos.

Entonces, ¿Cuál es el propósito detrás de la creación de los números imaginarios? En realidad, el número "i" se introdujo para abordar ecuaciones que carecían de soluciones reales en el conjunto de números reales.
En matemáticas, es incorrecto afirmar que una ecuación no puede resolverse, ya que esto depende del conjunto de números que estamos considerando.
Aquí tienes dos ejemplos:
- La ecuación x + 8 = 1 no tiene solución en el conjunto de números naturales (donde x es igual a -7), pero sí en el conjunto de números relativos.
- La ecuación x² = 2 (x = raíz de 2) no puede ser resuelto en el conjunto de números racionales, pero sí en el conjunto de números irracionales.
¿Y por qué no imaginar que 2 + 2 es 10?
De hecho, el número imaginario "i" ha desempeñado un papel crucial en la resolución de ecuaciones en diversos campos de las matemáticas. Su introducción ha permitido resolver todo tipo de ecuaciones, ya sean de números enteros, irracionales o decimales.
El impacto del número imaginario "i" va más allá de las matemáticas y ha sido fundamental en la investigación en física y electricidad. En particular, ha sido esencial en el estudio de los circuitos impresos de los ordenadores, sentando las bases de la revolución informática del siglo XX.
La incorporación de los números complejos e imaginarios ha ampliado nuestras capacidades para resolver problemas que de otro modo carecerían de respuesta. Estos números han sido especialmente útiles en la resolución de integrales y en el tratamiento de problemas sin solución previa a su introducción.
Los números complejos son ampliamente utilizados por los ingenieros en diversos campos como la acústica, electrónica, aerodinámica, hidrodinámica, entre otros. Estos números son especialmente útiles en el análisis de formas de onda y flujos, así como en el desarrollo de tecnologías como radares, imágenes y sonares.
En el ámbito de la ingeniería electrónica, los números complejos permiten describir de manera precisa y eficiente el comportamiento de los circuitos electrónicos, lo que resulta fundamental para su diseño y funcionamiento.
Descubre también la historia de los números primos.
¿Te gustaría ofrecer clases de matemáticas en línea?
¿Dónde aprender el número "i"?
¿Deseas mejorar tus habilidades en Matemáticas, adentrarte en el fascinante mundo de los números imaginarios y complejos, y explorar el desafío de la abstracción necesaria para comprenderlos?
Encuentra al profesor perfecto de Matemáticas en Superprof Perú, donde podrás elegir entre una amplia variedad de profesores inscritos en Perú que ofrecen clases particulares a domicilio.
Si prefieres una opción más económica, también puedes optar por lecciones en línea a través de diversos sitios web, canales de video y tutoriales que brindan recursos educativos en Matemáticas.
Khan Academy
En esta plataforma educativa, tendrás la oportunidad de explorar a fondo el mundo de las Matemáticas, incluyendo un enfoque completo sobre los números complejos a través de lecciones teóricas y videos instructivos.
Encontrarás repasos detallados sobre conceptos como las raíces cuadradas, el número imaginario i, las raíces elevadas a la potencia de números negativos en el conjunto de números complejos, el valor cuyo cuadrado es -52 (por ejemplo), las potencias de i, etc.
YouTube
Al realizar una búsqueda en la barra de búsqueda de YouTube con las palabras clave "número i", encontrarás una amplia selección de videos que te ayudarán a comprender este número imaginario.
Dado que los cálculos con números imaginarios pueden parecer complicados, estos videos te recordarán que el número i es un concepto matemático diseñado para simplificar los cálculos.
Encontrarás numerosos videos de acceso gratuito relacionados con el número i, lo cual te permitirá realizar ejercicios interactivos de Matemáticas sin sentir la presión de tener a un profesor observándote de cerca.
Lee también nuestro artículo sobre los números perfectos.
Estudio de caso con el número "i"

Vamos a analizar el uso del número i de manera concreta. Tomemos una fórmula sencilla y expliquemos las diferentes etapas de razonamiento, teniendo en cuenta la introducción del álgebra: a + bi. En esta expresión, las letras "a" y "b" representan números reales, mientras que "i" se refiere a la unidad imaginaria. ¿Cómo se realiza el cálculo?
Cuando estamos realizando una suma o una resta, llevamos a cabo la operación matemática separando las partes reales de las partes imaginarias, obteniendo así:
(2 + 3i) + (4 + 5i) = 6 + 8i
Cuando realizamos una multiplicación entre dos números complejos, aplicamos la regla de la distributividad y la propiedad i^2 = -1. Veamos un ejemplo para ilustrar este proceso:
(2 + 3i ) × (4 + 5i) = 8 + 10i + 12i + 15i² = -7 + 22i
Para realizar divisiones con números complejos, utilizamos el método del conjugado. En este método, multiplicamos tanto el numerador como el denominador por el "conjugado" del segundo número complejo y luego simplificamos el resultado. El conjugado de un número complejo a + bi es el número a - bi. Veamos un ejemplo para comprenderlo mejor:
2 + 3i sobre 4 + 5i = (2 + 3i) (4-5i) sobre (4 = 5i) (4 - 5i)
= 8 - 10i + 12i - 15i al cuadrado sobre 4 al cuadrado - (5i) al cuadrado
= 23 + 2i sobre 16 + 25
= 23 de 41 + 2 sobre 41i
Es altamente recomendable que practiques manualmente antes de aprender a utilizar una calculadora para trabajar con números complejos. Es fundamental familiarizarse con las reglas y el razonamiento científico detrás de ellos antes de depender completamente de la calculadora. Para ayudarte en este proceso, te animamos a explorar los mejores recursos disponibles para mejorar tus habilidades en el manejo de números complejos.
Entonces, ¿es tan complicado?
¿Conoces el número áureo?
Recursos en línea para aprender los números puros imaginarios
La gran ventaja de Internet es la amplia variedad de recursos disponibles para estudiar, repasar y aprender matemáticas, incluyendo los números complejos e imaginarios. En la red, puedes encontrar una amplia gama de recursos relacionados con este tema. A continuación, te presento algunos ejemplos:
- Sitios especializados en la enseñanza, como Aula fácil, que ofrece contenido en matemáticas.
- Sitios especializados en la enseñanza de las Matemáticas, como Vitutor, donde encontrarás soluciones de aprendizaje concretas para los números complejos.
- Sitios para establecer contacto con profesores de Matemáticas, como nuestra plataforma Superprof Perú, que te permite beneficiarte del apoyo personalizado según tu nivel.
- Sitios de ejercicios en línea de Matemáticas, tanto de contenido oficial (exámenes oficiales) como de contenido nuevo (asociaciones de matemáticas).
En cuanto a los recursos de enseñanza general en línea, son especialmente útiles si estás comenzando a familiarizarte con los números complejos y los descubres por primera vez en matemáticas. Estos recursos suelen ofrecer fórmulas básicas de números imaginarios y ejercicios diseñados para ayudarte a adquirir los conceptos fundamentales.
Si deseas llevar tu conocimiento al siguiente nivel, existen sitios web especializados en matemáticas que pueden ofrecerte contenido más avanzado. Por ejemplo, en matesfacil.com, encontrarás material adaptado a diferentes niveles, ya sea principiante, intermedio o avanzado. Estos recursos a menudo ofrecen ejercicios interactivos que brindan retroalimentación inmediata sobre tus respuestas, junto con comentarios que te ayudarán a comprender el razonamiento detrás de ellas. Estos tipos de recursos son ideales para repasar conceptos básicos o fortalecer tus conocimientos sobre números imaginarios.
Si deseas profundizar en tu comprensión de los números imaginarios o los números imaginarios puros, es altamente recomendable buscar un profesor particular de matemáticas. La razón es simple: los profesores particulares poseen un conocimiento avanzado de matemáticas y pueden proporcionarte las claves para comprender estos números complejos, así como explicarte el funcionamiento de los exámenes de matemáticas en diferentes contextos, como por ejemplo, en oposiciones. La mayoría de estos profesores han pasado por experiencias similares y su experiencia resulta muy valiosa para orientarte en tu proceso de aprendizaje.
En plataformas como Superprof Perú, puedes realizar una búsqueda basada en dos factores: nivel de conocimiento y ubicación geográfica. Esto te permite encontrar rápidamente un profesor que se adapte a tus necesidades y que esté cercano a tu localidad, lo que facilita el acceso a clases presenciales.
Una vez que hayas adquirido los fundamentos de los números imaginarios y hayas fortalecido tus conocimientos, es útil recurrir a plataformas de ejercicios de matemáticas. Estos recursos son ideales para practicar de manera regular o intensiva en áreas específicas de las matemáticas, como el álgebra, y son especialmente útiles cuando te estás preparando para un examen.
Además, puedes considerar realizar un curso intensivo de matemáticas centrado en los números imaginarios. Estos cursos suelen estar disponibles durante las vacaciones escolares, en la universidad o a través de asociaciones educativas. Participar en un curso intensivo te brinda la oportunidad de sumergirte de lleno en el tema, recibir una instrucción más detallada y enfocada, y acelerar tu aprendizaje.
¿Estás en la búsqueda de un profesor particular de matemáticas en Perú?
¿Cómo repasar los números imaginarios puros?

Si bien los recursos en línea son una excelente opción para explorar y comprender los números complejos, es importante destacar que los recursos en formato impreso también son muy útiles para el estudio de las matemáticas. Los libros con ejercicios específicos sobre números complejos y las presentaciones que incluyen fórmulas matemáticas adaptadas son especialmente valiosos.
Aunque es cierto que los exámenes se realizan en papel y no en una computadora, es beneficioso acostumbrarse al uso de recursos impresos para prepararse adecuadamente.
Aquí tienes algunos ejemplos de libros de referencia para estudiar los números complejos y los números imaginarios:
- Una introducción a los números complejos, de Francisco Rivero Mendoza.
- Números complejos y sus aplicaciones a la geometría, de I.M. Yaglom.
- Números complejos: Álgebra, de Christiam Manuel Huertas Ramírez.
- Números reales y números complejos, de Roberto Benavent De La Cámara.
- Trigonometría y números complejos, de José Colera Jiménez et al.
Existen obras generales que abordan los números complejos y están dirigidas tanto a estudiantes y principiantes en matemáticas como a entusiastas de este tema. Estas obras proporcionan una introducción general a los números complejos y también exploran casos concretos con números imaginarios.
Descubrir los números complejos no es una tarea difícil, gracias a la amplia variedad de recursos disponibles en el campo de las matemáticas. Puedes encontrar el recurso que mejor se adapte a tu nivel y objetivos, ya sea contactando con personas adecuadas, como tu profesor de secundaria, para solicitar clases de apoyo o pedir recomendaciones de recursos para mejorar tu aprendizaje.
Si necesitas ponerte al día antes de un examen o unas oposiciones, te recomendamos que varíes los recursos: ¡en papel, en línea y un profesor!
Entonces, ¿tú qué opinas sobre los números imaginarios y los números complejos? ¿Cuáles son tus consejos para aprender a dominarlos?
La respuesta a la pregunta «¿qué número se obtiene si se eleva el número 3i al cuadrado?» es -9 (porque (3i) ² = 3² x i² = 9 i², entonces i² = -1).
Y para «¿cuál de estos dos números tiene -16 como cuadrado (-4 o 4i)?», es 4i porque la raíz de -16 es imaginaria, así que es 4i.
¿Buscas clases particulares de matemáticas en Perú?
Resumir con IA:















