La multiplicación de números racionales es uno de los pilares fundamentales en el aprendizaje matemático, especialmente en la etapa de educación secundaria y en los primeros niveles de estudios universitarios relacionados con ciencias exactas. Esta operación, aunque a primera vista parece sencilla, encierra una gran riqueza conceptual que va mucho más allá de memorizar pasos o fórmulas. Comprender cómo y por qué se multiplican números racionales de determinada manera permite al estudiante desarrollar una comprensión más profunda de las matemáticas y aplicarlas con mayor seguridad y versatilidad.
Dominar la multiplicación de racionales no solo permite resolver ejercicios escolares comunes en clases de aritmética o álgebra, sino que también ofrece herramientas prácticas para enfrentar una amplia variedad de situaciones en la vida real. ¡Y para eso es este artículo!
En esta guía completa, exploraremos paso a paso el significado profundo de esta operación, su lógica interna, sus diferentes aplicaciones prácticas y cómo se integra con otros temas del currículo matemático.
Hoy comprenderás por qué es fundamental para calcular porcentajes en compras o finanzas, determinar el área de figuras geométricas en proyectos de construcción o arquitectura, y resolver problemas que involucran fracciones de cantidades, como en recetas de cocina o mediciones científicas. Además, permite interpretar y manipular datos estadísticos de manera más efectiva, algo crucial en una sociedad cada vez más orientada hacia el análisis de la información.
También presentaremos diversos ejemplos concretos, ejercicios resueltos, propiedades fundamentales, errores comunes que se deben evitar y recomendaciones prácticas para que estudiantes, docentes y cualquier persona interesada puedan dominar este contenido con confianza y claridad:

¿Qué son los números racionales?
Los números racionales son aquellos que pueden expresarse como el cociente entre dos números enteros, es decir, en la forma a/b, donde "a" y "b" son enteros y "b" es distinto de cero. Esto incluye:
- Fracciones positivas: 3/4, 5/8
- Fracciones negativas: -2/3, -7/5
- Enteros: 1, -4 (pueden representarse como 1/1 o -4/1)
- Decimales exactos: 0,25 = 1/4
- Decimales periódicos: 0,333... = 1/3
Por tanto, todo entero, fracción o decimal finito o periódico es un número racional.
Conoce más de los números racionales ¡aquí!
Definición de la multiplicación de números racionales
Multiplicar números racionales consiste en combinar cantidades proporcionales mediante una regla muy clara: se multiplican los numeradores entre sí y luego los denominadores entre sí. Esta operación, conocida como la multiplicación de números racionales, da como resultado una nueva fracción que, en muchos casos, puede y debe ser simplificada. Esta es una definición fundamental que se enseña desde los primeros cursos de aritmética porque permite resolver de forma directa problemas con fracciones, decimales y enteros.
Cuando hablamos de racionales, nos referimos tanto a fracciones como a números decimales exactos o periódicos, lo que significa que este procedimiento aplica para múltiples representaciones numéricas. Si el resultado de la multiplicación incluye fracciones muy grandes, se puede simplificar dividiendo numerador y denominador por un factor común.

Es importante tener en cuenta los signos: el resultado será positivo si ambos factores tienen el mismo signo, y negativo si tienen signos opuestos. Por eso, al resolver cualquier ejercicio de multiplicación con números racionales, debes prestar atención a la regla de los signos.
Dominar esta técnica no solo permite resolver cálculos básicos, sino también avanzar en temas como la multiplicación y división de números naturales, la proporcionalidad y la resolución de ecuaciones. Es una habilidad esencial para aplicar en distintos contextos, desde problemas escolares hasta situaciones reales como escalas, porcentajes o conversiones de unidades.
Ejemplo:
(2/3) x (5/4) = (2x5)/(3x4) = 10/12 = 5/6
Este resultado es una fracción irreducible, y como vemos, no hace falta buscar un denominador común como sucede en la suma o la resta.

¿Cómo se resuelve la multiplicación de números racionales?
Veamos el proceso paso a paso:
- Convertir a fracciones: Si hay decimales o mixtos, primero conviértelos a fracciones impropias.
- Multiplicar numeradores: Multiplica todos los números de la parte superior.
- Multiplicar denominadores: Haz lo mismo con la parte inferior.
- Aplicar signos: Determina si el resultado será positivo o negativo.
- Simplificar el resultado: Reduce la fracción a su mínima expresión.
Ejemplo con signos:
(-3/5) x (2/3) = -6/15 = -2/5
Ejemplo con decimales:
0.6 x 3/4 = (3/5) x (3/4) = 9/20
Multiplicacion de numeros racionales de 3 fracciones
No importa cuántas fracciones se estén multiplicando: se aplica el mismo procedimiento.
Ejemplo:
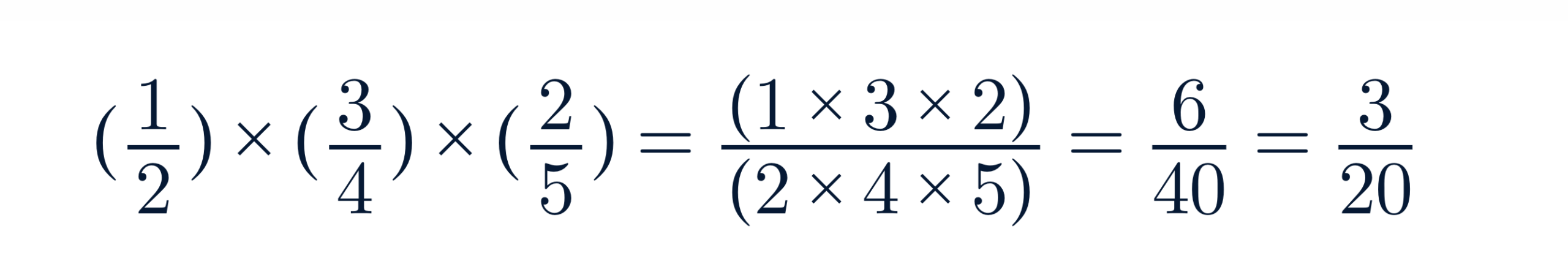
Este tipo de operaciones es común cuando resolvemos problemas con tasas, proporciones o porcentajes sucesivos.
Manejo de signos: positivo o negativo
Saber aplicar correctamente los signos es vital:
- Positivo x Positivo = Positivo
- Negativo x Negativo = Positivo
- Positivo x Negativo = Negativo
- Negativo x Positivo = Negativo
Ejemplo:
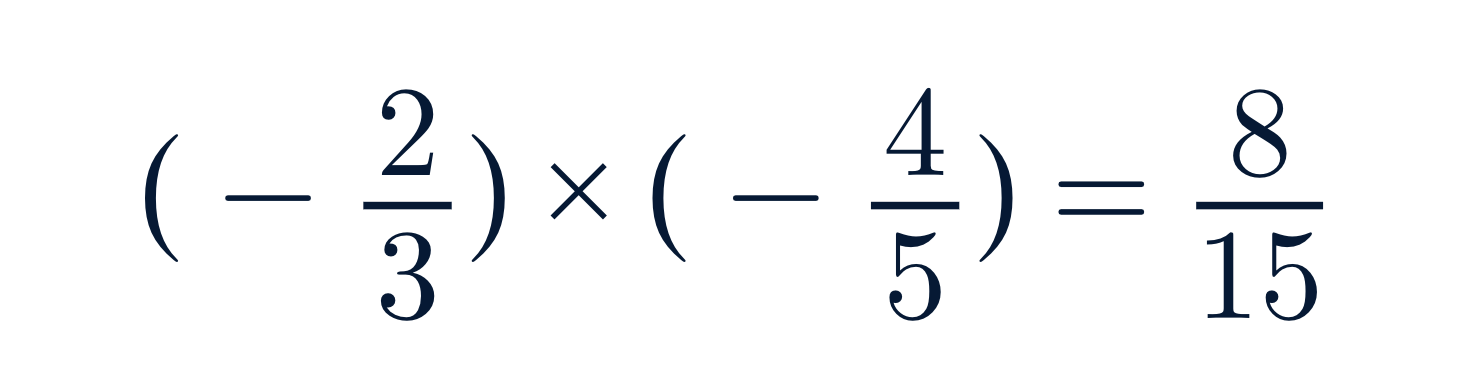
El resultado es positivo porque el producto de dos números negativos da un valor positivo.
Propiedades de la multiplicación de racionales
Las propiedades de la multiplicación de racionales son:
- Conmutativa: a x b = b x a
- Asociativa: (a x b) x c = a x (b x c)
- Elemento neutro: a x 1 = a
- Elemento absorbente: a x 0 = 0
- Inverso multiplicativo: a x (1/a) = 1 (siempre que a ≠ 0)
No te pierdas algunos ejemplos de números racionales en la vida cotidiana.
Ejercicios: 5 ejemplos de multiplicación de números racionales
Ejemplo 1: (4/7) x (3/5) = 12/35
Ejemplo 2: (-2/3) x (5/8) = -10/24 = -5/12
Ejemplo 3: (3/4) x (-2/5) = -6/20 = -3/10
Ejemplo 4: (1/6) x (0,4) = (1/6) x (2/5) = 2/30 = 1/15
Ejemplo 5: (5/9) x (3/2) = 15/18 = 5/6
Problemas de multiplicación de números racionales
Problema 1: Una receta requiere 2/3 de taza de azúcar por porción. ¿Cuánta azúcar necesito para 3/2 porciones?
Solución: (2/3) x (3/2) = 6/6 = 1 taza
Problema 2: Un alumno recorre 3/5 de kilómetro en un minuto. ¿Cuánto recorrerá en 4/3 minutos?
Solución: (3/5) x (4/3) = 12/15 = 4/5 km
Problema 3: Una botella contiene 3/4 de litro. Si se llena 2/5 veces, ¿cuánta cantidad se usó?
Solución: (3/4) x (2/5) = 6/20 = 3/10 litro
Multiplicación y división de números naturales
Antes de aprender sobre racionales, los estudiantes deben dominar la multiplicación y división de números naturales. Estas operaciones básicas funcionan como el puente hacia las fracciones. Comprender cómo se distribuyen los factores, cómo se simplifican los productos y qué ocurre al dividir un entero entre otro es clave para abordar problemas más complejos.
Ejemplos multiplicacion y division de números naturales:
6 x 4 = 24
24 / 6 = 4
Luego se extiende a:
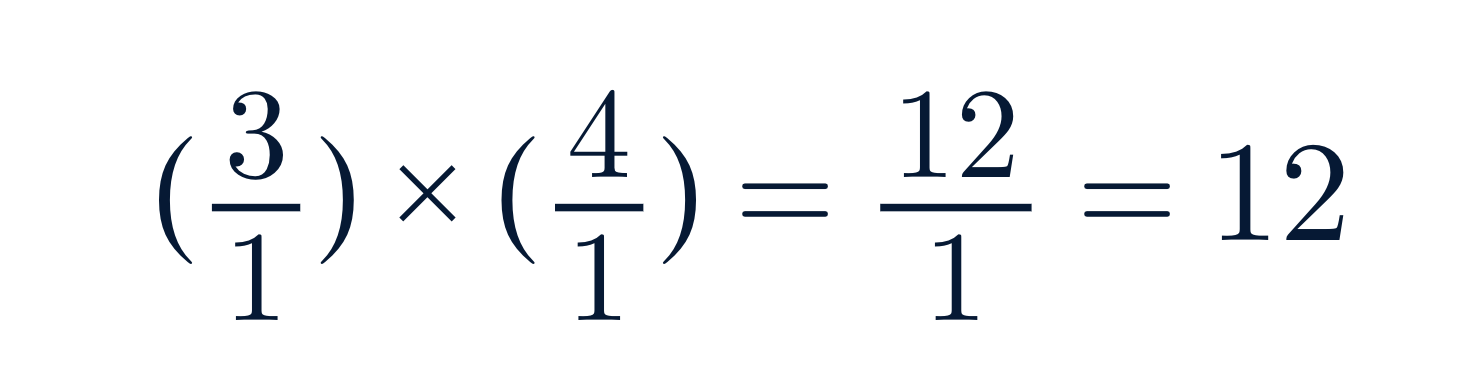
Números racionales: ejemplos de suma, resta, multiplicación y división
Suma: 1/2 + 1/3 = (3 + 2)/6 = 5/6
Resta: 3/4 - 1/2 = (3 - 2)/4 = 1/4
Multiplicación: 2/3 x 5/7 = 10/21
División: (4/5) ÷ (2/3) = (4/5) x (3/2) = 12/10 = 6/5
¿Qué tanto conoces de la operaciones combinadas? Descúbrelo ¡aquí!
Consejos para resolver multiplicaciones de racionales
Para que no se te olvide el orden de los pasos ni los aspectos clave al resolver multiplicaciones de fracciones, puedes usar una palabra clave fácil de recordar: FRACC. Esta palabra no solo está relacionada con el tema, sino que cada letra te recuerda una estrategia fundamental:
F → Fracciona todo primero
👉 Convierte todos los números (decimales, mixtos, enteros) a fracciones antes de operar.
R → Reduce al mínimo
👉 Simplifica numeradores y denominadores antes y después de multiplicar para evitar fracciones enormes.
A → Atiende los signos
👉 Revisa con cuidado si el resultado debe ser positivo o negativo. Signo correcto = resultado correcto.
C → Calcula con propiedades
👉 Usa propiedades como la conmutativa y la asociativa para reorganizar y resolver más rápido.
C → Combina variedad en tus ejercicios
👉 Practica con decimales, fracciones mixtas, negativas y positivas. ¡La práctica te da confianza!
También: Descubre cómo se realiza la la adición o sustracción de fracciones ¡aquí!
Dominar la multiplicación de números racionales no es solo una competencia matemática más; es una puerta de entrada a una comprensión más profunda de la lógica numérica y de las herramientas fundamentales que usamos a diario, tanto dentro como fuera del aula. Esta operación, que a veces se subestima por su aparente simplicidad, tiene aplicaciones prácticas que van desde las finanzas personales hasta la resolución de problemas complejos en ciencia, tecnología o ingeniería.

Cuando entiendes cómo multiplicar fracciones, convertir decimales en racionales o manejar los signos correctamente, estás fortaleciendo tu pensamiento lógico y desarrollando habilidades de razonamiento que te servirán durante toda la vida. Saber multiplicar números racionales no solo te prepara para los desafíos académicos del presente, sino que te da herramientas para tomar decisiones más informadas en tu vida cotidiana.
A lo largo de este texto, hemos repasado definiciones clave, propiedades esenciales, reglas prácticas y muchos ejemplos para que el proceso se vuelva más claro y accesible. Pero más allá de memorizar fórmulas, lo verdaderamente importante es comprender el “por qué” de cada paso. Esta comprensión profunda es la que permite avanzar hacia temas más complejos con confianza.
Y si en algún momento sientes que necesitas una mano amiga que te guíe, recuerda que en Superprof puedes encontrar docentes especializados que no solo explican, sino que te ayudan a razonar, practicar y mejorar tu desempeño paso a paso. Ya sea que estés en colegio, universidad o simplemente quieras retomar tu camino matemático, hay alguien dispuesto a ayudarte con clases personalizadas, dinámicas y enfocadas en tus objetivos.
¡No te detengas! Sigue multiplicando tu conocimiento, tu comprensión y tus habilidades. Las matemáticas pueden ser exigentes, pero también son una poderosa aliada si las haces tuyas.
Resumir con IA: