Las operaciones combinadas implican la ejecución de distintas operaciones matemáticas (como suma, resta, multiplicación, división, y a veces exponentes y paréntesis) ¡en un solo enunciado! Al solucionar operaciones combinadas, el orden en que efectuamos los cálculos es fundamental para obtener resultados correctos.
Por ello, existen reglas de las operaciones combinadas que marcan prioridades claras: primero los paréntesis (o corchetes, llaves si corresponde), luego multiplicaciones y divisiones, y por último suma y resta. Estas normas ayudan a reducir los enunciados antes de efectuar los cálculos.
En este texto aprenderás:

- Cuáles son los pasos para solucionar operaciones combinadas.
- Cómo simplificar y efectuar cálculos con numerador, denominador y signos.
- Varias formas de practicar mediante operaciones combinadas ejercicios, especialmente de operaciones combinadas de adición y resta para primaria.
- Algunos ejemplos detallados sobre como solucionar operaciones combinadas y las diferencias según el contexto (instrucción en educación básica o nivel medio).
- Asimismo veremos operaciones combinadas suma y resta, ecuaciones combinadas, y más.
Pero antes, descubre qué son los números racionales ¡aquí!

¿Qué son las operaciones combinadas?
Una operación combinada se compone de varias operaciones matemáticas en una misma expresión. En lugar de solo sumar o restar, se integran multiplicaciones, divisiones, y a veces exponentes. Por ejemplo:
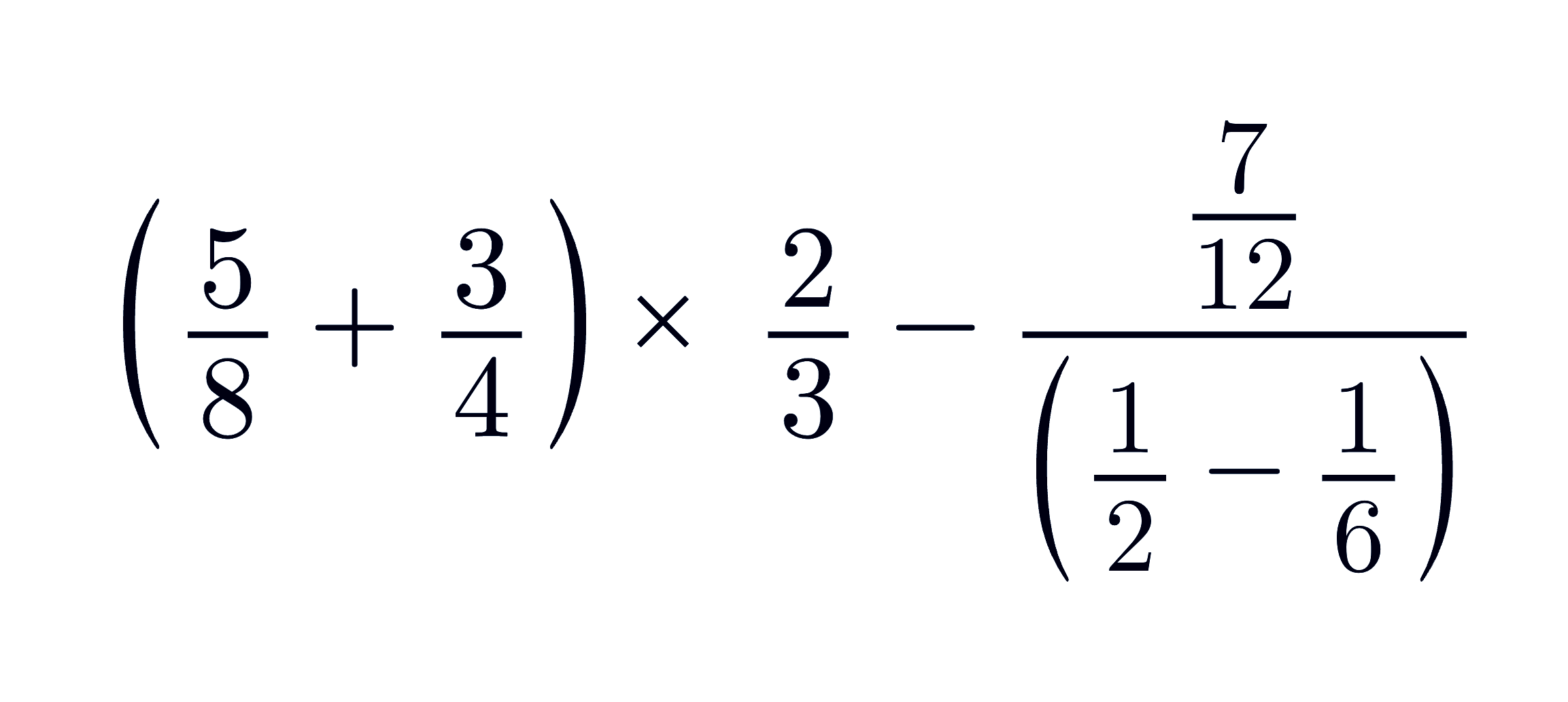
Este enunciado mezcla suma, resta, multiplicación y división. Para como se resuelven las operaciones combinadas, es indispensable conocer las reglas de las operaciones combinadas.
Ejemplos de números racionales aplicados a la vida diaria.
Reglas y jerarquía
Para solucionar operaciones combinadas, debemos seguir el orden:
- Solucionar paréntesis, corchetes y llaves (de adentro hacia afuera).
- Realizar multiplicación y división (en orden de izquierda a derecha).
- Finalmente, efectuar la suma y resta (de izquierda a derecha).
Estas normas conforman lo que conocemos como jerarquía matemática o regla PEMDAS (P, E, M, D, A, S). Es decir, primero Paréntesis, luego Exponentes (si los hay), después Multiplicación/División, y al final Adición/Sustracción. Así, como solucionar operaciones combinadas nunca puede prescindir del estudio de su secuencia.
Ahora, ¿sabes cómo funciona la multiplicación y división de números racionales?
Pasos para resolver correctamente
¿Te cuesta saber por dónde empezar cuando ves una operación larga y llena de fracciones o paréntesis? No te preocupes, solucionar operaciones combinadas es más sencillo de lo que parece si sigues un orden paso a paso. Aquí te explicamos cómo hacerlo de forma clara y sin enredos:
🔍 Lee con calma toda la expresión.
Antes de empezar a operar, observa bien qué tipo de operaciones hay: ¿suma? ¿resta? ¿multiplicación? ¿hay fracciones con numerador y denominador? ¿aparecen paréntesis? Este primer paso es clave para no saltarte nada importante.
( ) Empieza siempre por los paréntesis, corchetes o llaves.
Si hay expresiones encerradas, resuélvelas primero. Si hay varios niveles (por ejemplo, paréntesis dentro de corchetes), ve desde adentro hacia afuera. Recuerda que los paréntesis mandan.
✖ Dentro de los paréntesis, prioriza multiplicaciones y divisiones.
Nada de sumar o restar de frente. Primero multiplica y divide lo que haya dentro, y luego suma o resta. ¡El orden cambia todo!
💡Una vez fuera de los paréntesis, sigue con las multiplicaciones y divisiones externas.
Cuando termines con lo que estaba encerrado, revisa qué multiplicaciones o divisiones siguen por fuera, siempre de izquierda a derecha.
➕Al final, haz las sumas y restas.
Ya con lo demás resuelto, ahora sí toca sumar y restar, también de izquierda a derecha. Este es el último paso antes del resultado.
📉 Si hay fracciones, trata de simplificarlas en cada paso.
Reducir fracciones usando el máximo común divisor (MCD) hace que los cálculos sean más fáciles y limpios. Así no te pierdes entre números enormes.
⚠️ Ojo con los signos.
Un signo mal colocado puede cambiar por completo el resultado. Fíjate bien si estás restando un número negativo o sumando un número con signo. ¡Eso puede hacer toda la diferencia!

¿Cómo realizar la suma y resta en fracciones?
Seguir estos pasos no solo te ayuda a solucionar bien, sino también a evitar errores comunes. Así, poco a poco, verás que entender cómo se resuelven las operaciones combinadas no solo es posible, ¡sino que puede ser hasta entretenido!
Ejemplo didáctico: primaria (operaciones combinadas de suma y resta para primaria)
Para alumnos de primaria, es común practicar operaciones combinadas suma y resta sencillas. Por ejemplo:
7 + 3 − 2 + 4 − 5
Esto es uno de los ejercicios de operaciones combinadas de adición y resta, sin paréntesis ni multiplicación/división. Para como solucionar operaciones combinadas de este tipo:
- Leemos la operación de izquierda a derecha.
- Efectuamos cada paso:
- 7 + 3 = 10 ⇒ con 10 − 2 = 8
- 8 + 4 = 12 ⇒ con 12 − 5 = 7
El resultado final es 7. En este contexto, es una operación combinada de adición y resta para primaria perfecta para practicar antes de avanzar a combinaciones más complejas.
Ejemplo intermedio: fracciones
Un nivel siguiente es incluir fracciones. Por ejemplo:
2/3 + 1/3 × 4
¿Por qué no sumamos 2/3 + 1/3 + 4? Porque primero se efectua la multiplicación:
- 1/3 × 4 = 4/3
- Luego sumamos 2/3 + 4/3 = 6/3 = 2
Este es un claro ejemplo de como se resuelven las operaciones combinadas cuando hay mezcla de adición y multiplicación. Primero multiplicamos, luego sumamos. Si hubiera paréntesis habría que resolverlos antes.

Ejemplo avanzado: combinación múltiple con paréntesis
Consideremos ahora un ejercicio más complejo que incluye paréntesis:
(5/8 + 3/4) × 2/3 − 7/12 ÷ (1/2 − 1/6)
Paso 1: resolver dentro de paréntesis
- Primer paréntesis: 5/8 + 3/4 = 5/8 + 6/8 = 11/8
- Segundo paréntesis: 1/2 − 1/6 = 3/6 − 1/6 = 2/6 = 1/3
La expresión queda:
(11/8) × 2/3 − 7/12 ÷ (1/3)Paso 2: multiplicación y división
- 11/8 × 2/3 = 22/24 = 11/12 (podemos simplificar antes: 2 y 8 comparten factor 2, quedan 11/4 × 1/3 = 11/12).
- 7/12 ÷ 1/3 = 7/12 × 3/1 = 21/12 = 7/4
La expresión se convierte en:
11/12 − 7/4
Paso 3: suma o resta
Convertimos fracciones al mismo denominador (12):
7/4 = 21/12
⇒ 11/12 − 21/12 = −10/12 = −5/6
Resultado: −5/6.
Este resumen muestra pasos para solucionar operaciones combinadas en un ejercicio que involucra paréntesis, división, multiplicación, suma/resta y fracciones.
Ecuaciones combinadas
Existen situaciones en que las combinaciones incluyen también ecuaciones combinadas, es decir, una igualdad con operaciones múltiples:
2(x + 3) − 3/2 = 5 × (x − 1/4)
Aunque esto implica álgebra, los pasos para solucionar operaciones combinadas son similares:
- Distribuir la multiplicación sobre sumas/restas dentro de paréntesis.
- Agrupar términos semejantes.
- Solucionar fracciones si las hay.
- Reducir y despejar la variable “x”.
Aunque las operaciones combinadas llegan al álgebra, los mismos principios de jerarquía y simplificación siguen vigentes.
Reglas de signos
Al solucionar operaciones combinadas, es esencial considerar los signos correctamente:
- (+) − (+) = resta habitual
- (+) − (−) = suma
- (−) − (+) = negativa
- (−) − (−) = suma negativa
Estas reglas se aplican al trabajar con números racionales, especialmente con fracciones donde el signo puede estar en el numerador o fuera de él. Al practicar debes prestar atención a ese detalle.
Consejos para practicar
Para afianzar estos conceptos:
- Practicar con muchos operaciones combinadas ejercicios, desde nivel básico hasta avanzado.
- Antes de efectuar cálculos complejos, reducir las fracciones usando MCD.
- Revisar la correcta resolución de paréntesis, corchetes y llaves.
- Identificar claramente el numerador y denominador, asegurando su simplificación antes de operar.
- Confirmar que los signos estén bien colocados en cada paso.
- Hacer autoevaluaciones explicando cada paso en voz o escrita: “primero simplifico…, luego multiplico…, finalmente sumo…”
Si te cuesta seguir el ritmo a las matemáticas por cuenta propia, recuerda que en Superprof tienes a un profesor experto ¡siempre a un click de ti!
Sea que estés en Lima, Huancayo, Arequipa, Cusco o cualquier parte del Perú, puedes aprender a dominar los números, procedimientos y fórmulas junto a los mejores profesores particulares de tu ciudad. Así, podrás reforzar tus conocimientos matemáticos, aprender nuevos principios o dominar operaciones específicas con fracciones, números racionales, dividendos y más...

Ejercicio para practicar
Aquí tienes un ejercicio para solucionar operaciones combinadas paso a paso:
(3/5 − 2/3) × (4 − 1/2) ÷ (6/7 + 1/7) + 5/2
- Solucionar paréntesis interiores:
- 3/5 − 2/3 = (9/15 − 10/15) = −1/15
- 4 − 1/2 = 7/2
- 6/7 + 1/7 = 7/7 = 1
- Reemplazar la expresión:
(−1/15) × (7/2) ÷ 1 + 5/2
- Multiplicar y dividir:
(−7/30) ÷ 1 = −7/30
- Sumar:
−7/30 + 5/2 = −7/30 + 75/30 = 68/30 = 34/15
Respuesta: 34/15.
Importancia y aplicaciones
Dominar las operaciones combinadas es clave tanto en la escuela como en la vida diaria:
- En primaria, apoyan los primeros pasos hacia el álgebra.
- En el día a día, al resolver descuentos, problemas financieros, fraccionarios, y cálculo de proporciones en recetas, se aplican las mismas reglas.
- Si más adelante estudias matemáticas avanzadas, las ecuaciones combinadas se vuelven más frecuentes, y dominar estos procedimientos básicos es esencial para progresar.
Dominar las operaciones combinadas es esencial para avanzar en el aprendizaje matemático, ya que permiten solucionar cálculos que integran múltiples operaciones en una sola expresión. Para enfrentarlas correctamente, es indispensable seguir un orden específico: primero los paréntesis, luego las multiplicaciones y divisiones, y finalmente las sumas y restas. Este procedimiento garantiza resultados correctos y coherentes.
Además, antes de efectuar cualquier operación, es recomendable reducir las fracciones reduciendo el numerador y el denominador, lo cual facilita los cálculos y evita errores comunes. También es fundamental prestar atención a los signos, ya que un pequeño descuido puede alterar por completo el resultado.
Los pasos para solucionar operaciones combinadas son claros y aplicables en distintos niveles educativos, desde problemas sencillos de adición y resta para primaria hasta expresiones más complejas con fracciones o incluso ecuaciones combinadas. Existen numerosos ejercicios que puedes practicar para fortalecer tu comprensión y agilidad en este tema. Con constancia y atención a las reglas, solucionar este tipo de operaciones se convierte en una habilidad sólida y confiable.
Resumir con IA:















